場合の数・並べ方

場合の数では、$ABC$の$3$種類のカードを並べ替えると、何通りの並べ方ができるか、というような問題を解くコツを学びます。

重複を許す場合・許さない場合で組み合わせの数がかわってきます。文章問題からどちらの場合の数を質問されているのか、みわけられるようにしましょう。

場合の数・並べ方

並べかた問題とは...重複を許す並び替えが何通りあるか

例えば$A$さん$B$さんの$2$人$1$組のチームでリレーを走るとき、$A$さんが先に走る場合と$B$さんが先に走る場合の二種類あります。どちらの場合でも$A$さん$B$さんは出場しますが、走る順番が違いますのでどちらもカウントするのが並べ方です。

並べかたの問題の特徴は、「$ABC$という$3$枚のカードを並び替えると、何通りの組み合わせができるか」というようなものです。樹形図を書いて調べます。

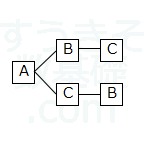
$A$が一番左端にくる場合は、$ABC$、$ACB$の$2$種類。
$B$が一番左にくる場合は、$BAC$、$BCA$の$2$種類
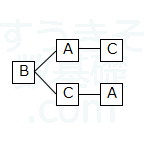
$C$が一番左にくる場合は$CAB$、$CBA$の$2$種類です。

上のように樹形図を全部書く必要はありません。最初の一つだけ書ければ、あとはかけ算で答えが出ます。

樹形図は全部で$3$種類、各樹形図は$2$種類の組み合わせができますので、$3\times2=6$となり答えは$6$種類です。

最初の一つ（上の図では$A$が一番左にくる樹形図）を書いてあとは先頭になる種類の数をかけ算すれば答えを出す事ができます。

組み合わせ方問題とは重複を許さないペアが何通りあるか

例えば野球の対戦は何通りあるかで考えるのが組み合わせ方です。$ABCD$の$4$チームが出場するとき、$A$対$B$も$B$対$A$も同じ試合です。このように意味が同じな組み合わせを除いて数えるのが組み合わせ方の数え方です。

実際に下に$ABCD$の対戦の組み合わせを書いてみると、$1$行目最初の$AB$と、$2$行目最初の$BA$は、同じチームの対戦です。同じ意味の試合になりますからこれらはカウントしません。

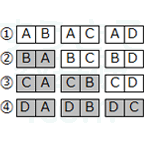
結果は$6$通りの組み合わせになることがわかりますね。

$ABCDEFG$の計$7$人から$6$人を選ぶとき、何通りの組み合わせがありますか。

樹形図を書いて考えても良いですが、$7$人のうちいつも一人だけ選ばれません。この人が選ばれない場合を考えるとすぐに答えが出ます。

1. $A$が選ばれない場合　$=\ \ BCDEFG$
2. $B$が選ばれない場合　$=A\ \ CDEFG$
3. $C$が選ばれない場合　$=AB\ \ DEFG$
4. $D$が選ばれない場合　$=ABC\ \ EFG$
5. $E$が選ばれない場合　$=ABCD\ \ FG$
6. $F$が選ばれない場合　$=ABCDE\ \ G$
7. $G$が選ばれない場合　$=ABCDEF\ \ $

以上のことから、選ばれないものに着目するとすぐに答えを出すことができます。

$7$通り