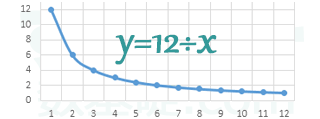反比例
反比例は比例の逆で、片方が2倍、3倍になったとき、もう一方は$\displaystyle{\frac{1}{2}}$倍、$\displaystyle{\frac{1}{3}}$倍になることを言います。
反比例とは反比例とは...片方が2倍、3倍になったとき、もう一方は$\displaystyle{\frac{1}{2}}$倍、$\displaystyle{\frac{1}{3}}$倍になる
反比例の式...$y=a\div{x}$ ($a$は決まった数) 例: $y=12\div{x}$
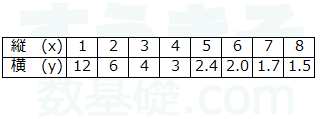
この$a=$決まった数は、表の上下をかけ算します。下の表なら、一番左からこのような計算になります。
$1\times12=12\\[5pt] 2\times6=12\\[5pt] 3\times4=12\\[5pt] 4\times3=12\\[5pt] 5\times2.4=12 $
どこをかけ算しても同じ答えになります。すなわち「決まった数」となります。
面積$12cm^2$の板は、縦の長さが$1cm$の時横は$12cm$、縦$2cm$のとき横$6cm$のようになります。縦の長さをを$x$、横の長さを$y$としたとき、式は$y=12\div{x}$です。
反比例のグラフ...なめらかな曲線
反比例の文章問題...かけ算して全体を出してから割り算し$x$をだす
時速$40km$で$3$時間かかる道のりを、時速$30km$で走ったら何時間かかりますか。
問題を読むと、ある道のりを違うスピードで走ったらどのくらい時間がかかるのかを聞いています。この文章問題で、道のりは同じであることがわりますね。道のりが「決まった数」となるわけです。
速度の問題がきたら「今日は掃除だ!」を思い出します。今日のキョは距離のキョ、掃除のソは速度のソ、掃除のジは時間のジ。
この式に数字を当てはめて、「決まった数」(道のり)を出しましょう。$40\times3=120km$
次に$y=a\div{x}$の式に数字をあてはめます。時速$40km$で$3$時間かかるものが、時速$50km$ならもっと時間が短くなり、時速$60km$ならさらに短くなり...という反比例の問題です。
$x$と$y$を使った式は$y=120\div{x}$ですね。$x$には速度が入ります。質問では時速$30km$で走ったら何分かかるかをきいているので、$x$に時速$30km$を代入すれば答えがわかります。
$ y=120\div{30}\\[5pt] y=4 $
$4$時間